The function performs a non-linear regression using the first-order multi-target model. The model equation is: $$\frac{S}{S_0}=1-(1-e^{-k\,t})^m$$ where \(S/S_0\) is the fraction of surviving molecules, \(k\) is the average number of hits per time unit, \(m\) is the number of hits required to degrade the molecule, and \(t\) is time.
Arguments
- dtframe
A data-frame containing 2 or 3 columns: time, normalized concentration and error (optional), respectively
Value
Returns the results of the regression as a nls object.
Details
The FOMT model has been proposed as an alternative to the Weibull equation that is commonly used when the time-dependent behavior of the data significantly deviates from that predicted by standard chemical models.
Examples
t <- c(0, 4, 8, 12, 16, 20)
conc <- c(1, 0.98, 0.99, 0.67, 0.12, 0.03)
err <- c(0.02, 0.05, 0.04, 0.04, 0.03, 0.02)
dframe <- data.frame(t, conc, err)
FOMT <- FOMT(dframe)
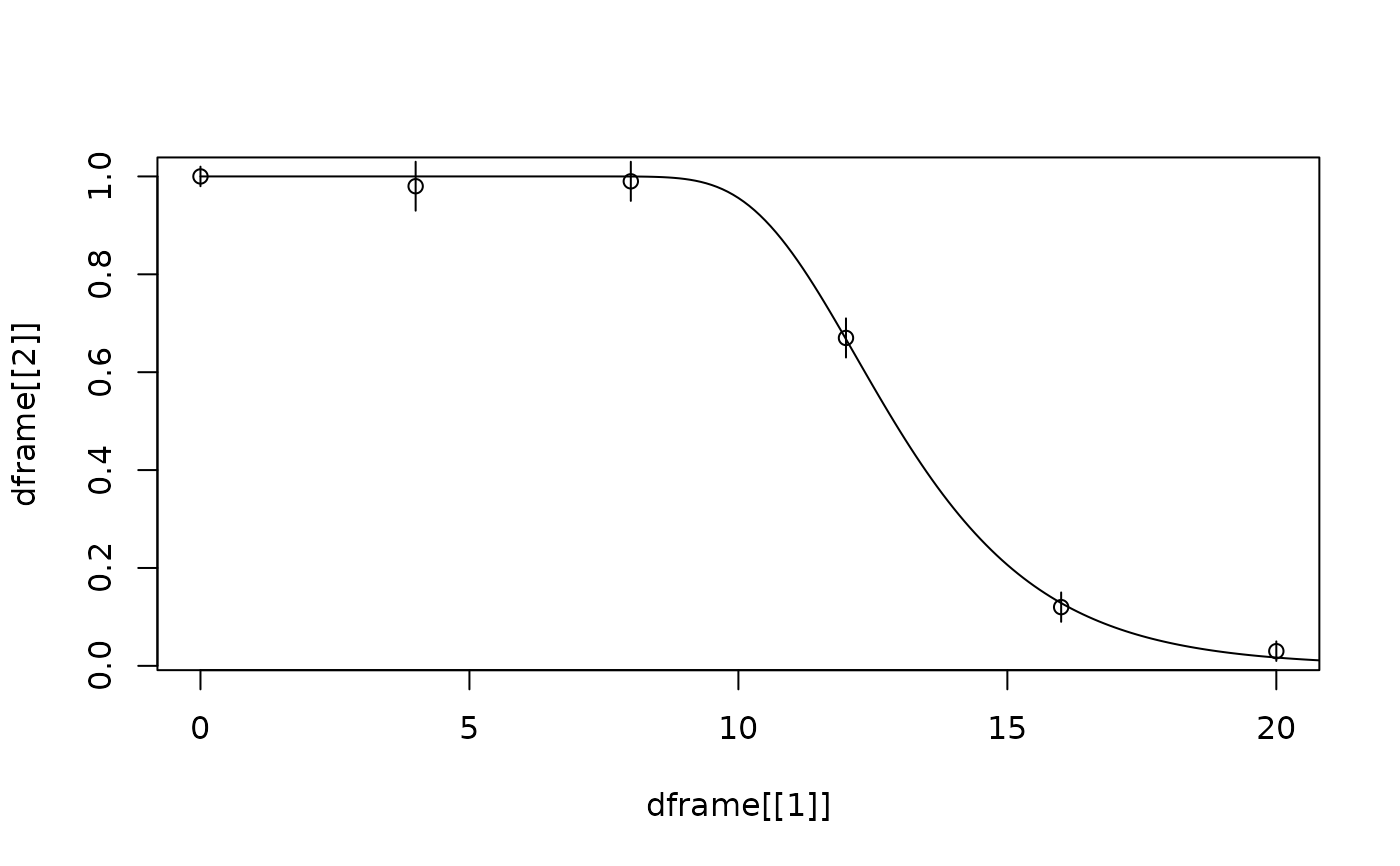
plot(dframe[[1]], dframe[[2]])
arrows(dframe[[1]], dframe[[2]] + dframe[[3]],
dframe[[1]], dframe[[2]] - dframe[[3]],
length = 0
)
newt <- seq(0, 21, by = 0.1)
lines(newt, predict(FOMT, newdata = list(t = newt)))
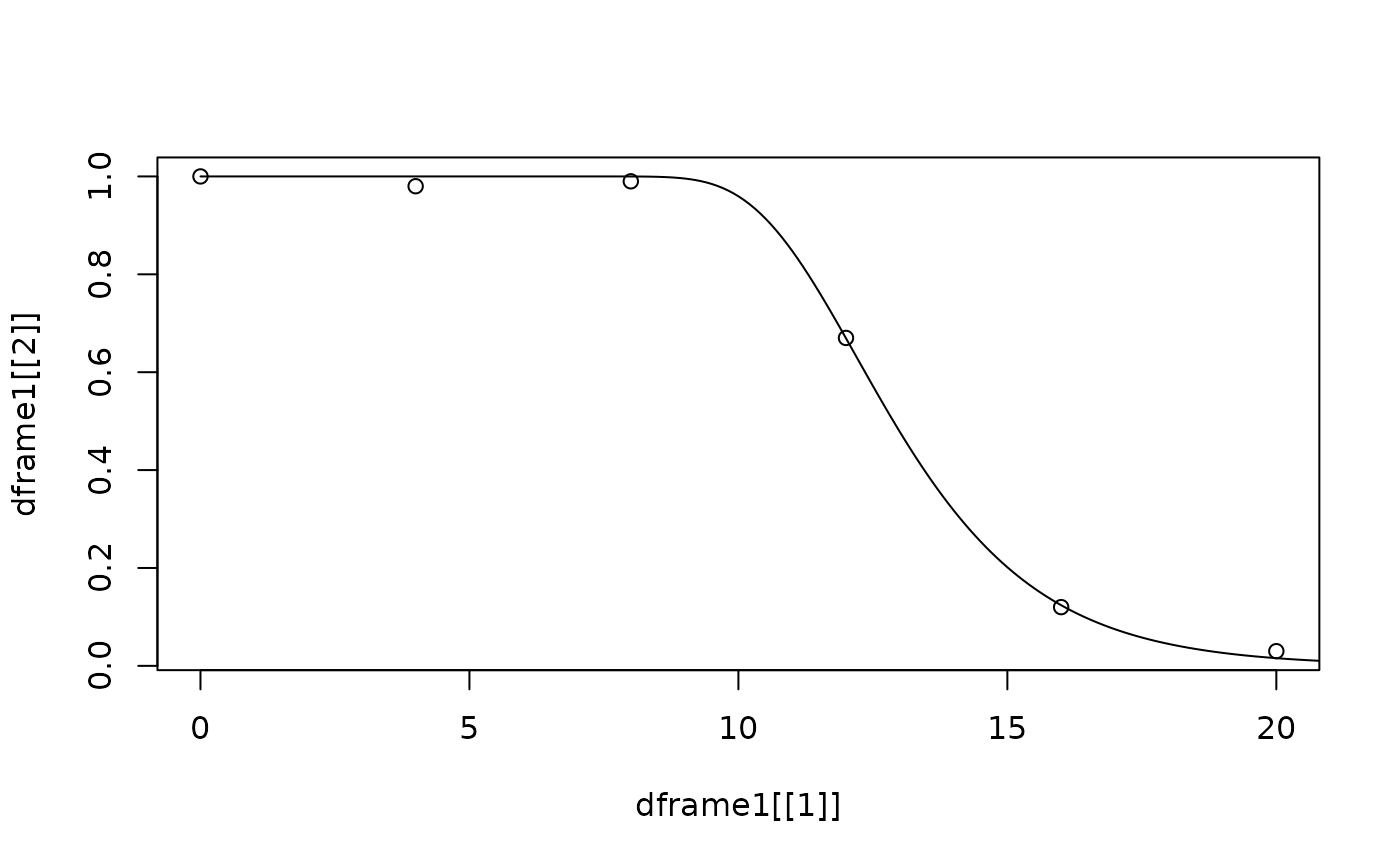
dframe1 <- data.frame(t, conc)
FOMT1 <- FOMT(dframe1)
plot(dframe1[[1]], dframe1[[2]])
lines(newt, predict(FOMT1, newdata = list(t = newt)))
summary(FOMT)
#>
#> Formula: y ~ 1 - (1 - exp(-k * t))^n
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> k 0.52026 0.02686 19.372 4.19e-05 ***
#> n 565.99854 194.55448 2.909 0.0437 *
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 0.4256 on 4 degrees of freedom
#>
#> Number of iterations to convergence: 10
#> Achieved convergence tolerance: 1.439e-07
#>
summary(FOMT1)
#>
#> Formula: y ~ 1 - (1 - exp(-k * t))^n
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> k 0.53083 0.02934 18.090 5.49e-05 ***
#> n 645.79131 235.80495 2.739 0.052 .
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 0.0134 on 4 degrees of freedom
#>
#> Number of iterations to convergence: 12
#> Achieved convergence tolerance: 5.236e-06
#>